数据结构与算法笔记

本篇文章将介绍数据结构与算法的基本概念（前端版）。

去年这个时间我在写数据结构与算法的博文，今年还在写，令人感叹。

基础

算法的基本概念

算法（Algorithm）是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制
也就是说，能够对一定规范的输入，在有限时间内获得所要求的输出
算法的五大特性：

有限性（Finiteness）：一个算法必须保证执行有限步之后结束
确切性（Definiteness）：一个算法的每一步骤必须有确切的定义
输入（Input）：一个算法有零个或多个输入，以刻画运算对象的初始情况，所谓零个输入是指算法本身给定了初始条件
输出（Output）：一个算法有一个或多个输出。没有输出的算法毫无意义
可行性（Effectiveness）：算法中执行的任何计算步骤都是可以被分解为基本的可执行的操作步骤，即每个计算步骤都可以在有限时间内完成（也称之为有效性

算法的复杂度

时间复杂度是指执行一个算法所需要的计算工作量，它反映了算法的执行效率和数据规模的关系。我们通常用大 O 符号来表示时间复杂度，例如$O(n)、O(log_n)、O(n^2)$等。时间复杂度越小，算法的效率越高。

空间复杂度是指执行一个算法所需要的内存空间，它反映了算法的存储开销和数据规模的关系。我们也用大 O 符号来表示空间复杂度，例如$O(1)、O(n)、O(n^2)$等。空间复杂度越小，算法的空间利用率越高。

查看常用排序算法的复杂度

排序算法	平均时间复杂度	最好情况	最坏情况	空间复杂度	排序方式	稳定性
冒泡排序	O(n²)	O(n)	O(n²)	O(1)	In-place	稳定
选择排序	O(n²)	O(n²)	O(n²)	O(1)	In-place	不稳定
插入排序	O(n²)	O(n)	O(n²)	O(1)	In-place	稳定
希尔排序	O(n log n)	O(n log² n)	O(n log² n)	O(1)	In-place	不稳定
归并排序	O(n log n)	O(n log n)	O(n log n)	O(n)	Out-place	稳定
快速排序	O(n log n)	O(n log n)	O(n²)	O(log n)	In-place	不稳定
堆排序	O(n log n)	O(n log n)	O(n log n)	O(1)	In-place	不稳定
计数排序	O(n + k)	O(n + k)	O(n + k)	O(k)	Out-place	稳定
桶排序	O(n + k)	O(n + k)	O(n²)	O(n + k)	Out-place	稳定
基数排序	O(n x k)	O(n x k)	O(n x k)	O(n + k)	Out-place	稳定

数据结构

栈与队列

栈是一种先进后出的线性表，JS中的数组可以实现一个栈（限定pop与push操作）。

class Stack {
  private stack: number[];
  private length: number;
  constructor(length: number) {
    this.length = length;
    this.stack = [];
  }
  pop() {
    if (!this.stack.length) {
      console.error("Stack is empty!");
      return;
    }
    console.log(this.stack.pop());
  }
  push(el: number) {
    if (this.stack[this.length - 1]) {
      console.error("Stack is full!");
      return;
    }
    this.stack.push(el);
  }
  peek() {
    if (!this.stack.length) {
      console.error("Stack is empty!");
      return;
    }
    return this.stack[this.stack.length - 1];
  }
}

查看栈的应用，表达式的计算

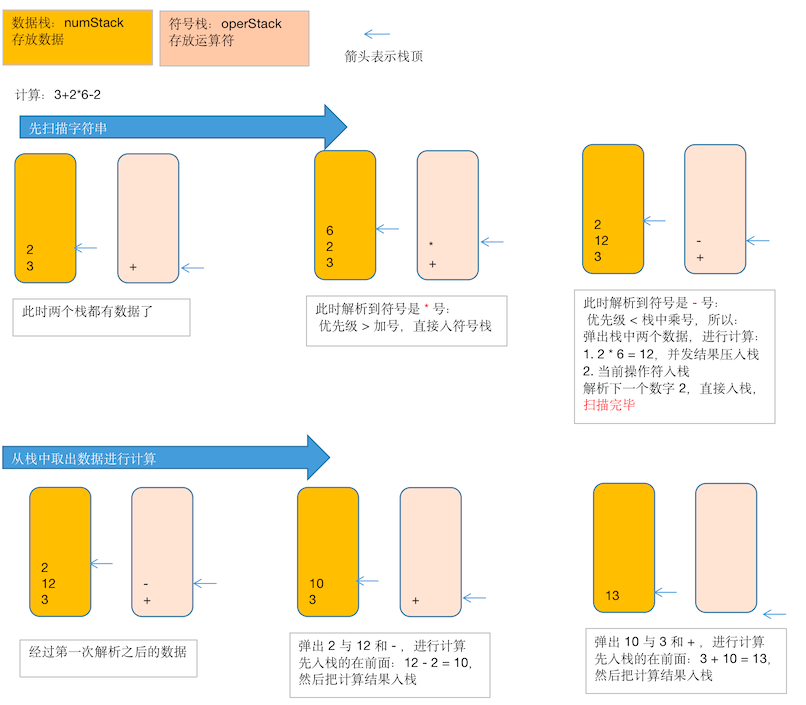
中缀表达式计算问题

前缀表达式求值过程

从 右到左 扫描表达式
遇到数字时，将数字压入堆栈
遇到 运算符 时
弹出栈顶的两个数（栈顶和次顶），用运算符对它们做相应的计算，并将结果入栈。
计算顺序是：先弹出来的 (运算符) 后弹出来的

然后重复以上步骤，直到表达式的最左端，最后运算出的值则是表达式的值。

看完前缀表达式的计算逻辑，那么你要明白的是，从一个 中缀表达式 转换为 前缀表达式 时，优先级顺序是已经处理好的，因为在求值时，不进行优先级的判定

例如：(3+4)x5-6 对应的前缀表达式为：- x + 3 4 5 6，前缀表达式求值步骤如下：

从右到左扫描，将 6、5、4、3 压入栈
遇到 + 运算符时：
将弹出 3 和 4（3 为栈顶元素，4 为次顶元素），计算出 3 + 4 = 7，将结果压入栈
遇到 x 运算符时
将弹出 7 和 5，计算出 7 x 5 = 35，将 35 压入栈
遇到 - 运算符时
将弹出 35 和 6，计算出 35 - 6 = 29，压入栈
扫描结束，栈中留下的唯一一个数字 29 则是表达式的值

后缀表达式（逆波兰表达式）

后缀表达式 又称为 逆波兰表达式，与前缀表达式类似，只是 运算符 位于 操作数之后。

比如：(3+4)x5-6 对应的后缀表达式 3 4 + 5 x 6 -

再比如：

中缀表达式	后缀表达式
`a + b`	`a b +`
`a + (b-c)`	`a b c - +`
`a+(b-c)*d`	`a b c - d * +`
`a+d*(b-c)`	`a d b c - * +`
`a=1+3`	`a 1 3 + =`

后缀表达式求值过程

从 左到右 扫描表达式
遇到数字时，将数字压入堆栈
遇到 运算符 时
弹出栈顶的两个数（栈顶和次顶），用运算符对它们做相应的计算，并将结果入栈。
计算顺序是：后弹出来的 (运算符) 先弹出来的

然后重复以上步骤，直到表达式的最右端，最后运算出的值则是表达式的值。

比如：(3+4)x5-6 对应的后缀表达式 3 4 + 5 x 6 -

从左到右扫描，将 3、4 压入堆栈
扫描到 + 运算符时
将弹出 4 和 3，计算 3 + 4 = 7，将 7 压入栈
将 5 入栈
扫描到 x 运算符时
将弹出 5 和 7 ，计算 7 x 5 = 35，将 35 入栈
将 6 入栈
扫描到 - 运算符时
将弹出 6 和 35，计算 35 - 6 = 29，将 29 压入栈
扫描表达式结束，29 是表达式的值

中缀表达式转后缀表达式

初始化两个栈：
- 运算符栈：s1
- 中间结果栈：s2
从左到右扫描中缀表达式
遇到操作数时，将其压入 s2
遇到运算符时
比较它与 s1 栈顶运算符的优先级：
1. 如果 s1 为空，或则栈顶运算符号为 ( ，则将其压入符号栈 s1
2. 如果：优先级比栈顶运算符高，也将其压入符号栈 s1
3. 如果：优先级比栈顶运算符 低或相等，将 s1 栈顶的运算符弹出，并压入到 s2 中

再重复第 4.1 步骤，与新的栈顶运算符比较（因为 4.3 将 s1 栈顶运算符弹出了）

这里重复的步骤在实现的时候有点难以理解，下面进行解说：

如果 s1 栈顶符号 优先级比 当前符号 高或则等于，那么就将其弹出，压入 s2 中（循环做，是只要 s1 不为空）
如果栈顶符号为 (，优先级是 -1，就不会弹出，就跳出循环了
跳出循环后，则将当前符号压入 s1
遇到括号时：
1. 如果是左括号 ( ：则直接压入 s1
2. 如果是右括号 )：
则依次弹出 s1 栈顶的运算符，并压入 s2，直到遇到 左括号 为止，此时将这一对括号丢弃
重复步骤 2 到 5，直到表达式最右端
将 s1 中的运算符依次弹出并压入 s2
依次弹出 s2 中的元素并输出，结果的逆序即为：中缀表达式转后缀表达式

下面进行举例说明：

将中缀表达式：1+((2+3)*4)-5 转换为后缀表达式

扫描到的元素	s2（栈底->栈顶）	s1（栈底->栈顶）	说明
`1`	`1`	`null`	遇到操作数直接压入 s2
`+`	`1`	`+`	`s1`为空，直接压入
`(`	`1`	`+ (`	运算符为`(`，直接压入
`(`	`1`	`+ ( (`	运算符为`(`，直接压入
`2`	`1 2`	`+ ( (`	遇到操作数直接压入 `s2`
`+`	`1 2`	`+ ( ( +`	栈顶元素为`(`，直接压入 `s1`
`3`	`1 2 3`	`+ ( ( +`	遇到操作数直接压入 s2
`)`	`1 2 3 +`	`+ (`	遇到`)`时，依次弹出 s1栈顶的运算符，并压入 s2 直到遇到左括号为止，此时将这一对括号丢弃
`*`	`1 2 3 +`	`+ ( *`	栈顶元素为`(`，直接压入`s1`
`4`	`1 2 3 + 4`	`+ ( *`	遇到操作数直接压入 `s2`
`)`	`1 2 3 + 4 *`	`+`	遇到`)`时，依次弹出 s1栈顶的运算符，并压入 s2 直到遇到左括号为止，此时将这一对括号丢弃
`-`	`1 2 3 + 4 * +`	`-`	优先级比栈顶运算符低或者相等，则弹出 s1栈顶元素，将其压入 s2 中，然后继续循环步骤 4，直至当前符号压入 s1
`5`	`1 2 3 + 4 * + 5`	`-`	遇到操作数直接压入 `s2`
`null`	`1 2 3 + 4 * + 5 -`	`null`	将 s1 的运算符依次弹出并压入 s2 ，结果的逆序即为：中缀表达式转后缀表达式的结果

由于 s2 是一个栈，弹出是从栈顶弹出，因此逆序后结果就是 1 2 3 + 4 * + 5 -

队列是一种先进先出的线性表，JS中的数组可以实现一个队列（限定push和shift操作）。

若要充分利用数组的空间，可实现一个环形队列的数据结构。
需要留一个空位的原因为：需要留出一个位置区分队列满与队列空的情况

队列为空：front === rear。
队列为满：(rear + 1) % maxSize === front。
队列长度：(rear - front + Maxsize) % maxSize。
队列遍历：从front累加size次，获取每次的arr[i % maxSize]的元素。
取队尾元素：注意考虑rear索引为0的情况。

const readline = require("readline");
const rl = readline.createInterface({
  input: process.stdin,
  output: process.stdout,
});
class CircleQueue {
  private maxSize: number;
  private front: number;
  private rear: number;
  private arr: number[];
  constructor(maxSize: number) {
    this.maxSize = maxSize;
    this.front = 0;
    this.rear = 0;
    this.arr = new Array(maxSize);
  }
  isEmpty(): boolean {
    return this.rear === this.front;
  }
  isFull(): boolean {
    return (this.rear + 1) % this.maxSize === this.front;
  }
  add(el: number) {
    if (this.isFull()) {
      console.warn("队列已满");
      return;
    }
    this.arr[this.rear++] = el;
    this.rear = this.rear % this.maxSize;
  }
  get(): number | undefined {
    if (this.isEmpty()) {
      console.warn("队列为空");
      return;
    }
    const el = this.arr[this.front++];
    this.front = this.front % this.maxSize;
    return el;
  }
  head(): number | undefined {
    if (this.isEmpty()) {
      console.warn("队列为空");
      return;
    }
    return this.arr[this.front];
  }
  tail(): number | undefined {
    if (this.isEmpty()) {
      console.warn("队列为空");
      return;
    }
    return this.rear - 1 < 0
      ? this.arr[this.maxSize - 1]
      : this.arr[this.rear - 1];
  }
  show() {
    for (let i = this.front; i < this.size() + this.front; i++) {
      const index = i % this.maxSize;
      console.log(this.arr[index]);
    }
  }
  size() {
    return (this.rear + this.maxSize - this.front) % this.maxSize;
  }
}
const queue = new CircleQueue(4);
const switchInput = (input: string) => {
  switch (input) {
    case "s":
      queue.show();
      break;
    case "e":
      rl.close(); // 关闭 readline 实例
      break;
    case "a":
      rl.question("请输入一个数字", (line: string) => {
        queue.add(Number(line));
      });
      break;
    case "g":
      {
        const result = queue.get();
        result && console.log(result);
      }
      break;
    case "h":
      {
        const result = queue.head();
        result && console.log(result);
      }

      break;
    case "t":
      {
        const result = queue.tail();
        result && console.log(result);
      }

      break;
    case "p":
      console.log("空？" + queue.isFull());
      break;
    default:
      console.log("您输入了无效的字符，请重新输入");
  }
};
rl.question(
  "s(show): 显示队列\ne(exit): 退出程序\na(add): 添加数据到队列\ng(get): 从队列取出数据\nh(head): 查看队列头的数据\nt(tail): 查看队列尾的数据\np(isEmpty): 队列是否为空\n",
  (input: string) => {
    switchInput(input);
    rl.on("line", (line: string) => {
      switchInput(line);
    });
  }
);

链表

链表（Linked List）是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的，由一系列结点（链表中每一个元素称为结点）组成
每个结点包括两个部分：一个是存储数据元素的数据域，另一个是存储下一个结点地址的指针域
注意反转链表的基本操作：

保存当前节点的下个节点（防止下一个节点丢失）
将当前节点插入道链表的头部。
将保存的下个节点取出，然后循环

class ThiefNode {
  public no: number;
  private name?: string;
  public nickName?: string;
  public next: ThiefNode | null;
  constructor(no: number = 0, name?: string, nickname?: string) {
    this.no = no;
    this.name = name;
    this.nickName = nickname;
    this.next = null;
  }
  toString() {
    return this.no + (this.nickName || "HEAD");
  }
}

class LinkedList {
  private head: ThiefNode;
  constructor() {
    this.head = new ThiefNode();
  }
  add(el: ThiefNode) {
    let temp: ThiefNode = this.head;
    while (true) {
      if (temp.next === null) {
        temp.next = el;
        break;
      }
      if (el.no === temp.next.no) {
        console.warn("Element already exists!");
        return;
      }
      temp = temp.next;
    }
  }
  print() {
    let temp = this.head.next;
    while (true) {
      if (temp) {
        console.log(temp.toString());
        temp = temp.next;
      } else {
        break;
      }
    }
  }
  addByOrder(el: ThiefNode) {
    let temp = this.head;
    while (true) {
      if (temp.next === null) {
        temp.next = el;
        break;
      } else if (el.no === temp.no) {
        console.warn("Element already exists!");
        return;
      } else if (el.no < temp.next.no) {
        el.next = temp.next;
        temp.next = el;
        return;
      }
      temp = temp.next;
    }
  }
  update(no: number, nickName: string) {
    let temp = this.head.next;
    while (true) {
      if (temp === null) {
        console.warn("Thief not in this linked list!");
        break;
      }
      if (temp.no === no) {
        temp.nickName = nickName;
        break;
      }
      temp = temp.next;
    }
  }
  delete(no: number) {
    let temp = this.head;
    while (true) {
      if (temp.next === null) {
        console.warn("Thief not in this linked list!");
        break;
      }
      if (temp.next.no === no) {
        temp.next = temp.next.next;
        break;
      }
      temp = temp.next;
    }
  }
  length(): number {
    let temp = this.head.next;
    let count: number = 0;
    while (true) {
      if (temp !== null) {
        count++;
      } else {
        break;
      }
      temp = temp.next;
    }
    return count;
  }
  lastIndexOf(num: number) {
    const length = this.length();
    if (num > length) {
      console.warn("Index out of Range!");
    }
    const index = length - num;
    let temp = this.head;
    for (let i = 0; i <= index; i++) {
      temp = temp.next!;
    }
    return temp;
  }
  reverse() {
    let temp = this.head.next;
    const newHead = new ThiefNode();
    while (true) {
      if (temp !== null) {
        const next = temp.next;
        temp.next = newHead.next;
        newHead.next = temp;
        temp = next;
      } else break;
    }
    this.head.next = newHead.next;
  }
  reversePrint() {
    let temp = this.head.next;
    const stack: Array<string> = [];
    while (true) {
      if (temp !== null) {
        stack.push(temp.toString());
      } else {
        break;
      }
      temp = temp.next;
    }
    for (let i = 0; i < stack.length; i++) {
      console.log(stack[stack.length - i - 1]);
    }
  }
}
const test = () => {
  const hero1 = new ThiefNode(1, "Amamiya Ren", "Joker");
  const hero2 = new ThiefNode(2, "Ryuji Sakamoto", "Skull");
  const hero3 = new ThiefNode(3, "Anne Takamaki", "Panther");
  const hero4 = new ThiefNode(4, "Yusuke Kitagawa", "Fox");
  const singleLinkedList = new LinkedList();
  singleLinkedList.add(hero4); // 添加顺序提前
  singleLinkedList.add(hero2);
  singleLinkedList.add(hero1);
  singleLinkedList.add(hero3);
  singleLinkedList.add(hero3);
  singleLinkedList.delete(3);
  singleLinkedList.print();
  console.log(singleLinkedList.lastIndexOf(1).toString());
  console.log(singleLinkedList.lastIndexOf(2).toString());
  console.log(singleLinkedList.lastIndexOf(3).toString());
  console.log(singleLinkedList.length());
  singleLinkedList.reverse();
  singleLinkedList.print();
  singleLinkedList.reversePrint();
};

test();
export default LinkedList;

树

二叉树
二叉树是一种树形结构，它的特点是每个节点最多只有两个子树，分别称为左子树和右子树。二叉树是有序的，也就是说，左子树和右子树的位置是不能互换的。二叉树是一种递归定义的结构，即一个二叉树要么是空的，要么是由一个根节点和两个非空的子二叉树组成。二叉树中的每个元素也称为一个节点，节点包含一个数据元素和若干指向子树的指针。
分类
- 满二叉树：如果二叉树中除了叶子结点，每个结点的度都为 2。
- 完全二叉树：如果二叉树中除去最后一层节点为满二叉树，且最后一层的结点依次从左到右分布。

二叉树的遍历

前序遍历：顶点 -> 左节点 -> 右节点
中序遍历：左节点 -> 顶点 -> 右节点
后续遍历：左节点 -> 右节点 -> 顶点

class TreeNode {
  constructor(val, left, right) {
    this.val = val;
    this.left = left;
    this.right = right;
  }
  preOrder(root) {
    if (!root) return;
    console.log(root.val);
    this.preOrder(root.left);
    this.preOrder(root.right);
  }
  preOrderLoop(root) {
    if (!root) return;
    const stack = [root];
    while (stack.length) {
      const n = stack.pop();
      console.log(n.val);
      if (n.right) stack.push(n.right);
      if (n.left) stack.push(n.left);
    }
  }
  infixOrder(root) {
    if (!root) return;
    this.infixOrder(root.left);
    console.log(root.val);
    this.infixOrder(root.right);
  }
  infixOrderLoop(root) {
    if (!root) return;
    const stack = [];
    let p = root;
    while (stack.length || p) {
      while (p) {
        stack.push(p);
        p = p.left;
      }
      const n = stack.pop();
      console.log(n.val);
      p = n.right;
    }
  }
  postOrder(root) {
    if (!root) return;
    this.postOrder(root.left);
    this.postOrder(root.right);
    console.log(root.val);
  }
  postOrderLoop(root) {
    // 定义一个栈和一个结果数组
    let stack = [];
    // 定义一个变量来记录上一次弹出的节点
    let lastPopNode = null;
    // 当栈不为空或者当前节点不为空时，循环执行
    while (stack.length > 0 || root) {
      // 如果当前节点不为空，将其压入栈中，然后访问其左子节点
      if (root) {
        stack.push(root);
        root = root.left;
      } else {
        // 如果当前节点为空，说明左子树已经遍历完毕，取出栈顶节点
        root = stack[stack.length - 1];
        // 如果栈顶节点有右子节点，并且右子节点不是上一次弹出的节点，说明右子树还没有遍历，访问其右子节点
        if (root.right && root.right !== lastPopNode) {
          root = root.right;
        } else {
          // 否则，说明左右子树都已经遍历，弹出栈顶节点，将其值加入结果数组，更新上一次弹出的节点，将当前节点置为空
          root = stack.pop();
          console.log(root.val);
          lastPopNode = root;
          root = null;
        }
      }
    }
  }
}
const node1 = new TreeNode(1);
const node2 = new TreeNode(2);
const node3 = new TreeNode(3);
const node4 = new TreeNode(4);
const node5 = new TreeNode(5);
const node6 = new TreeNode(6);
const node7 = new TreeNode(7);

node1.left = node2;
node2.left = node3;
node2.right = node4;

node1.right = node5;
node5.left = node6;
node5.right = node7;

node1.postOrder(node1);

堆
堆是一棵完全二叉树，满足

堆中某个结点的值总是不大于或不小于其父结点的值
堆总是一棵完全二叉树

堆又可以分成最大堆和最小堆：

最大堆：每个根结点，都有根结点的值大于两个孩子结点的值
最小堆：每个根结点，都有根结点的值小于孩子结点的值

// 完全二叉树可以用数组来表示
class MinHeap {
  constructor() {
    // 存储堆元素
    this.heap = [];
  }
  // 获取父元素坐标
  getParentIndex(i) {
    return (i - 1) >> 1;
  }

  // 获取左节点元素坐标
  getLeftIndex(i) {
    return i * 2 + 1;
  }

  // 获取右节点元素坐标
  getRightIndex(i) {
    return i * 2 + 2;
  }

  // 交换元素
  swap(i1, i2) {
    const temp = this.heap[i1];
    this.heap[i1] = this.heap[i2];
    this.heap[i2] = temp;
  }

  // 查看堆顶元素
  peek() {
    return this.heap[0];
  }

  // 获取堆元素的大小
  size() {
    return this.heap.length;
  }
  // 插入元素
  insert(value) {
    this.heap.push(value);
    this.shifUp(this.heap.length - 1);
  }

  // 上移操作
  shiftUp(index) {
    if (index === 0) {
      return;
    }
    const parentIndex = this.getParentIndex(index);
    if (this.heap[parentIndex] > this.heap[index]) {
      this.swap(parentIndex, index);
      this.shiftUp(parentIndex);
    }
  }

  // 删除元素
  pop() {
    this.heap[0] = this.heap.pop();
    this.shiftDown(0);
  }

  // 下移操作
  shiftDown(index) {
    const leftIndex = this.getLeftIndex(index);
    const rightIndex = this.getRightIndex(index);
    if (this.heap[leftIndex] < this.heap[index]) {
      this.swap(leftIndex, index);
      this.shiftDown(leftIndex);
    }
    if (this.heap[rightIndex] < this.heap[index]) {
      this.swap(rightIndex, index);
      this.shiftDown(rightIndex);
    }
  }
}

图

在计算机科学中，图是一种抽象的数据类型，在图中的数据元素通常称为结点，V 是所有顶点的集合，E 是所有边的集合

如果两个顶点 v,w，只能由 v 向 w，而不能由 w 向 v，那么我们就把这种情况叫做一个从 v 到 w 的有向边。v 也被称做初始点，w 也被称为终点。这种图就被称做有向图

如果 v 和 w 是没有顺序的，从 v 到达 w 和从 w 到达 v 是完全相同的，这种图就被称为无向图

图的结构比较复杂，任意两个顶点之间都可能存在联系，因此无法以数据元素在存储区中的物理位置来表示元素之间的关系

常见表达图的方式有如下：

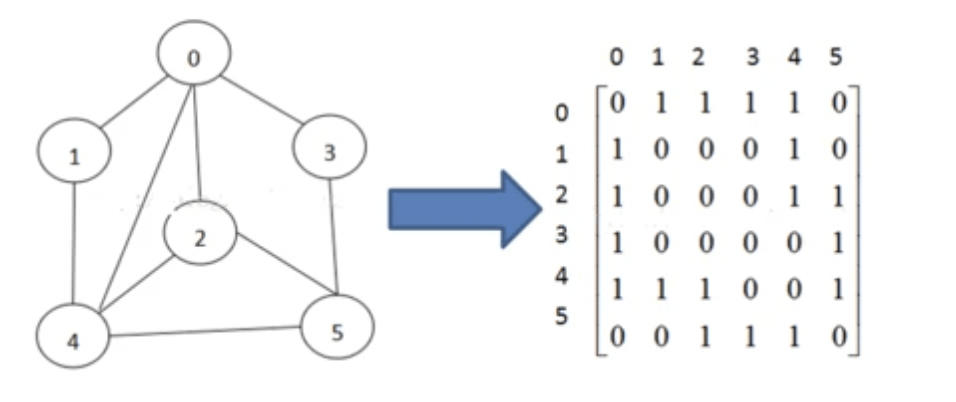
邻接矩阵
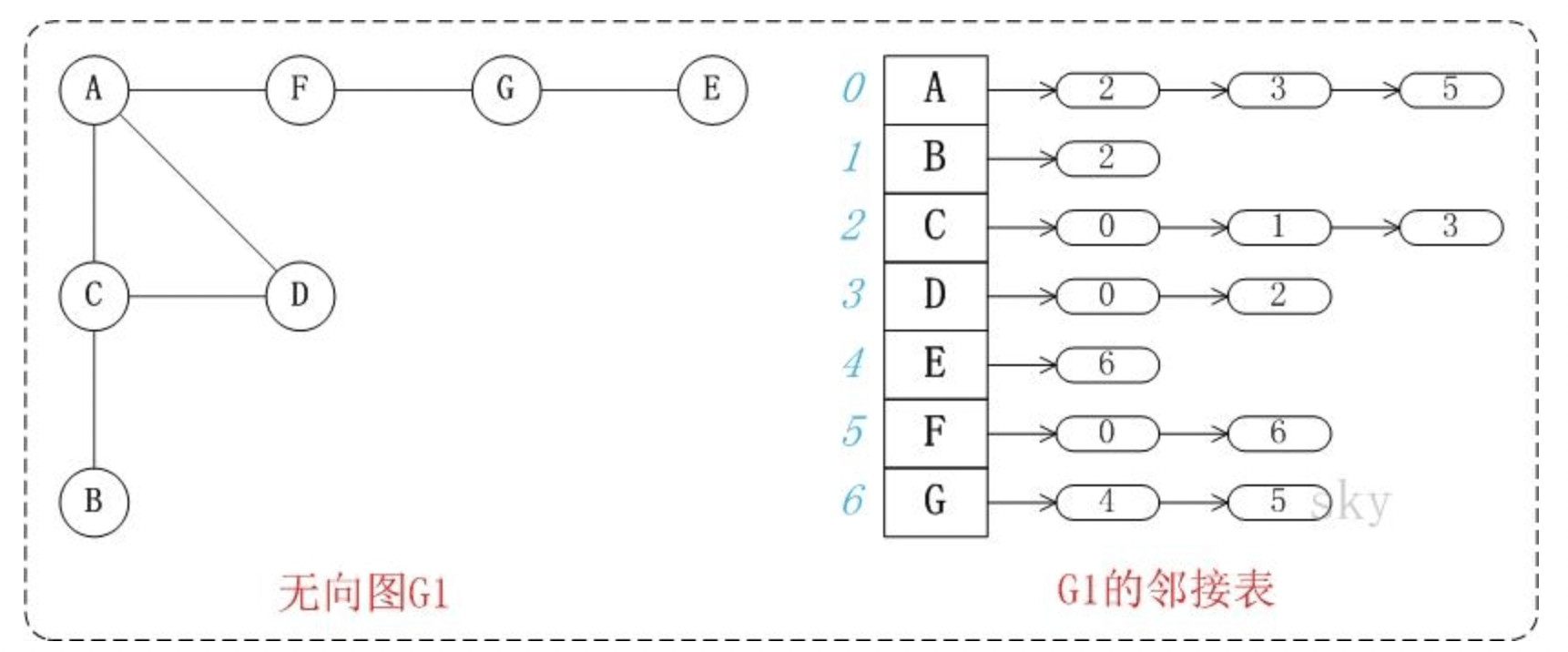
通过使用一个二维数组G[N][N]进行表示 N 个点到 N-1 编号，通过邻接矩阵可以立刻看出两顶点之间是否存在一条边，只需要检查邻接矩阵行 i 和列 j 是否是非零值，对于无向图，邻接矩阵是对称的。

邻接表

在JS中可以使用普通对象或者Map来表示

const graph = {
  A: [2, 3, 5],
  B: [2],
  C: [0, 1, 3],
  D: [0, 2],
  E: [6],
  F: [0, 6],
  G: [4, 5],
};

图的遍历

深度遍历：即遇到新节点就访问新节点，然后该节点上访问该节点的节点，也就是说尽可能往深处访问。
广度遍历：利用队列的数据结构。

const graph = {
  0: [1, 4],
  1: [2, 4],
  2: [2, 3],
  3: [],
  4: [3],
};

const visit1 = new Set();
const dfs = (n) => {
  console.log(n);
  visit1.add(n);
  graph[n].forEach((el) => {
    if (!visit1.has(el)) {
      dfs(el);
    }
  });
};

const visit2 = new Set();
const bfs = (n) => {
  visit2.add(n);
  const queue = [n];
  while (queue.length) {
    const n = queue.shift();
    console.log(n);
    graph[n].forEach((el) => {
      if (!visit2.has(el)) {
        visit2.add(el);
        queue.push(el);
      }
    });
  }
};

dfs(0);
console.log();
bfs(0);

常见算法

排序算法

冒泡排序

典中典，无需多言。

function bubbleSort(arr) {
  const len = arr.length;
  for (let i = 0; i < len - 1; i++) {
    for (let j = 0; j < len - 1 - i; j++) {
      if (arr[j] > arr[j + 1]) {
        // 相邻元素两两对比
        let temp = arr[j + 1]; // 元素交换
        arr[j + 1] = arr[j];
        arr[j] = temp;
      }
    }
  }
  return arr;
}

选择排序
同样经典，无需多言

function selectionSort(arr) {
  let len = arr.length;
  let minIndex, temp;
  for (let i = 0; i < len - 1; i++) {
    minIndex = i;
    for (let j = i + 1; j < len; j++) {
      if (arr[j] < arr[minIndex]) {
        // 寻找最小的数
        minIndex = j; // 将最小数的索引保存
      }
    }
    temp = arr[i];
    arr[i] = arr[minIndex];
    arr[minIndex] = temp;
  }
  return arr;
}

插入排序

const insertSort = (arr) => {
  const length = arr.length;
  let pre, current;
  for (let i = 1; i < length; i++) {
    pre = i - 1;
    current = arr[i];
    while (pre >= 0 && current < arr[pre]) {
      arr[pre + 1] = arr[pre];
      pre--;
    }
    arr[pre + 1] = current;
  }
  return arr;
};
console.log(insertSort([2, 5, 6, 2346, 56, 47, 567]));

归并排序

const mergeSort = (arr) => {
  const length = arr.length;
  if (length < 2) return arr;
  const middle = Math.ceil(length / 2);
  let left = arr.slice(0, middle),
    right = arr.slice(middle);
  return merge(mergeSort(left), mergeSort(right));
};

const merge = (left, right) => {
  const result = [];
  while (left.length && right.length) {
    if (left[0] <= right[0]) {
      result.push(left.shift());
    } else {
      result.push(right.shift());
    }
  }
  while (left.length) result.push(left.shift());
  while (right.length) result.push(right.shift());
  return result;
};
console.log(mergeSort([13, 27, 38, 49, 49, 65, 76, 97]));

快速排序

const quickSort = (arr) => {
  if (arr.length <= 1) return arr;
  const left = [];
  const right = [];
  const mid = arr[0];
  for (let i = 1; i < arr.length; i++) {
    if (arr[i] <= mid) {
      left.push(arr[i]);
    } else {
      right.push(arr[i]);
    }
  }
  return [...quickSort(left), mid, ...quickSort(right)];
};

const arr = quickSort([49, 38, 65, 97, 76, 13, 27, 49]);
console.log(arr);

查找算法

二分查找算法

const binarySearchFirst = (arr, target) => {
  if (arr.length < 1) return -1;
  let low = 0,
    high = arr.length - 1;
  while (low <= high) {
    const mid = Math.floor((low + high) / 2);
    if (target > arr[mid]) {
      low = mid + 1;
    } else if (target < arr[mid]) {
      high = mid - 1;
    } else {
      if (mid === 0 || arr[mid - 1] < arr[mid]) return mid;
      else high = mid - 1;
    }
  }
  return -1;
};
const binarySearchFirst2 = (arr, target, low = 0, high = arr.length) => {
  if (low > high) return -1;
  const mid = Math.floor((low + high) / 2);
  if (arr[mid] > target)
    return binarySearchFirst2(arr, target, low, mid - 1);
  else if (arr[mid] < target)
    return binarySearchFirst2(arr, target, mid + 1, high);
  else {
    if (mid === 0 || arr[mid - 1] < arr[mid]) return mid;
    return binarySearchFirst2(arr, target, low, mid - 1);
  }
};
console.log(binarySearchFirst2([13, 27, 38, 49, 49, 65, 76, 97], 65));

动态规划

01 背包和无限背包问题

// 01背包问题的js实现
function knapsack(w, v, W) {
  // w是物品重量数组，v是物品价值数组，W是背包总重量
  let n = w.length; // 物品个数
  let dp = new Array(W + 1).fill(0); // 初始化dp数组为全0
  for (let i = 0; i < n; i++) {
    // 遍历物品
    for (let j = W; j >= w[i]; j--) {
      // 逆向遍历背包容量
      dp[j] = Math.max(dp[j], dp[j - w[i]] + v[i]); // 状态转移方程
    }
  }
  return dp[W]; // 返回最大价值
}

function knapsack1(w, v, W) {
  // w是物品重量数组，v是物品价值数组，W是背包总重量
  let n = w.length; // 物品个数
  let dp = new Array(W + 1).fill(0); // 初始化dp数组为全0
  for (let i = 0; i < n; i++) {
    // 遍历物品
    for (let j = w[i]; j <= W; j++) {
      // 正向遍历背包容量
      dp[j] = Math.max(dp[j], dp[j - w[i]] + v[i]); // 状态转移方程
    }
  }
  return dp[W]; // 返回最大价值
}

// 测试用例
let w = [2, 3, 4]; // 物品重量数组
let v = [3, 4, 5]; // 物品价值数组
let W = 6; // 背包总重量
let expected = 8; // 期望的输出结果
let actual = knapsack1(w, v, W); // 实际的输出结果
console.log("Expected:", expected); // 打印期望的输出结果
console.log("Actual:", actual); // 打印实际的输出结果
console.log("Test passed:", expected === actual); // 比较期望和实际的输出结果，打印测试是否通过

回溯算法

八皇后问题

class Queen8 {
  private readonly N: number;
  private arr: Array<number>;
  private order: number;
  private print() {
    console.log(this.order + ":" + this.arr.join(" "));
  }
  constructor(N: number) {
    this.N = N;
    this.arr = Array.of(N).fill(0);
    this.order = 0;
  }
  private judge(row: number) {
    for (let i = 0; i < row; i++) {
      if (
        this.arr[i] === this.arr[row] ||
        row - i === Math.abs(this.arr[row] - this.arr[i])
      )
        return false;
    }
    return true;
  }
  public check(count: number) {
    if (count === this.N) {
      this.order++;
      this.print();
      return;
    }
    for (let i = 0; i < this.N; i++) {
      this.arr[count] = i;
      if (this.judge(count)) {
        this.check(count + 1);
      }
    }
  }
}

const queen = new Queen8(9);
queen.check(0);

约瑟夫环问题

数组实现

// 定义一个函数，接受两个参数：n 表示人数，m 表示报数的最大值
function josephus(n: number, m: number): number {
  // 创建一个长度为 n 的数组，用来存放每个人的编号，初始值为 1 到 n
  let arr: number[] = [];
  for (let i = 0; i < n; i++) {
    arr[i] = i + 1;
  }
  // 定义一个变量 index 来表示当前报数的人的索引，初始值为 0
  let index: number = 0;
  // 定义一个变量 count 来表示当前报数的值，初始值为 1
  let count: number = 1;
  // 定义一个变量 alive 来表示当前圆圈中还剩下的人数，初始值为 n
  let alive: number = n;
  // 使用一个循环，当 alive 大于 1 时，重复以下步骤
  while (alive > 1) {
    // 如果当前报数的人的编号不为 0 ，说明他还没有被淘汰，那么就判断 count 是否等于 m
    if (arr[index] !== 0) {
      // 如果 count 等于 m ，说明他要被淘汰，那么就将他的编号设为 0 ，并将 alive 减 1 ，将 count 重置为 1
      if (count === m) {
        arr[index] = 0;
        alive--;
        count = 1;
      } else {
        // 如果 count 不等于 m ，说明他还要继续报数，那么就将 count 加 1
        count++;
      }
    }
    // 将 index 加 1 ，并对 n 取模，以实现循环报数的效果
    index = (index + 1) % n;
  }
  // 最后，遍历数组，找到那个编号不为 0 的元素，它就是最后留下的那个人的编号
  for (let i = 0; i < n; i++) {
    if (arr[i] !== 0) {
      return arr[i];
    }
  }
  // 如果没有找到，返回 -1 表示出错
  return -1;
}

// 测试
console.log(josephus(5, 3)); // 输出 4
console.log(josephus(41, 3)); // 输出 31